Python实现简单的神经网络
在说神经网络之前,我们讨论一下神经元(Neurons),它是神经网络的基本单元。神经元先获得输入,然后执行某些数学运算后,再产生一个输出。比如一个2输入神经元的例子:在这个神经元里,输入总共经历了3步数学运算,先将输入乘以权重(weight):...
从零开始学习神经网络
搭建基本模块—神经元
在说神经网络之前,我们讨论一下神经元(Neurons),它是神经网络的基本单元。神经元先获得输入,然后执行某些数学运算后,再产生一个输出。比如一个2输入神经元的例子:
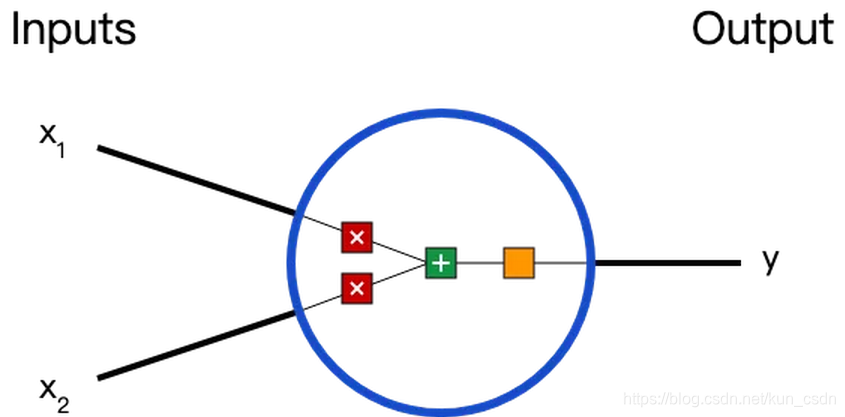
在这个神经元里,输入总共经历了3步数学运算,
先将输入乘以权重(weight):
x
1
→
x
1
∗
w
1
{x_1 \rightarrow x_1 * w_1}
x1→x1∗w1
x
2
→
x
2
∗
w
2
{x_2 \rightarrow x_2 * w_2}
x2→x2∗w2
(
x
1
∗
w
1
)
+
(
x
2
∗
w
2
)
+
b
{(x_1 * w_1) + (x_2 * w_2) + b}
(x1∗w1)+(x2∗w2)+b
最后经过激活函数(activation function)处理得到输出:
y
=
f
(
(
x
1
∗
w
1
)
+
(
x
2
∗
w
2
)
+
b
)
{y = f((x_1 * w_1) + (x_2 * w_2) + b)}
y=f((x1∗w1)+(x2∗w2)+b)
激活函数的作用是将无限制的输入转换为可预测形式的输出。一种常用的激活函数是sigmoid函数:
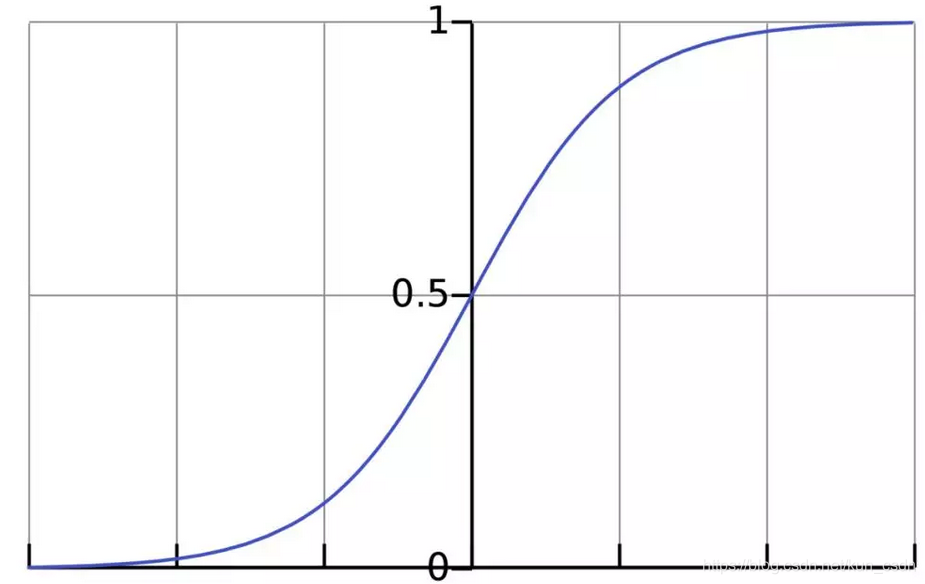
sigmoid函数的输出介于0和1,我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1,负向数值越大输出越接近0。
举个例子,上面神经元里的权重和偏置取如下数值:
w
=
[
0
,
1
]
;
b
=
4
{w = [0,1] ; b = 4}
w=[0,1];b=4
w
=
[
0
,
1
]
{w = [0,1]}
w=[0,1]是
w
1
=
0
,
w
2
=
1
{w_1=0, w_2=1}
w1=0,w2=1的向量形式写法。给神经元一个输入
x
=
[
2
,
3
]
{x=[2,3]}
x=[2,3],可以用向量点积的形式把神经元的输出计算出来:
w
∗
x
+
b
=
(
x
1
∗
w
1
)
+
(
x
2
∗
w
2
)
+
b
=
0
∗
2
+
1
∗
3
+
4
=
7
{w*x+b=(x_1*w_1)+(x_2*w_2)+b=0*2+1*3+4=7}
w∗x+b=(x1∗w1)+(x2∗w2)+b=0∗2+1∗3+4=7
y
=
f
(
w
∗
X
+
b
)
=
f
(
7
)
=
0.999
{y=f(w*X+b)=f(7)=0.999}
y=f(w∗X+b)=f(7)=0.999
以上步骤的Python代码是:
import numpy as np
def sigmoid(x):
# our activation function: f(x) = 1 / (1 * e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron():
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# weight inputs, add bias, then use the activation function
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4
n = Neuron(weights, bias)
# inputs
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
搭建神经网络
神经网络就是把一堆神经元连接在一起,下面是一个神经网络的简单举例:
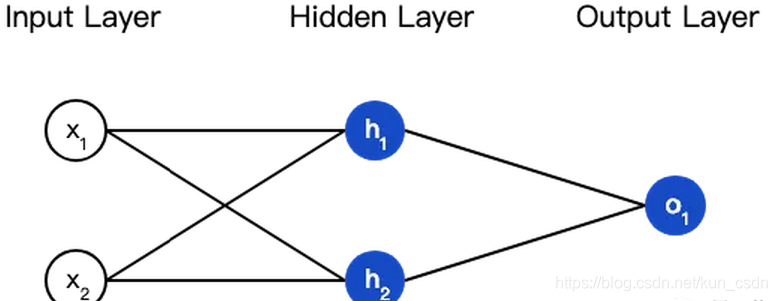
这个网络有2个输入、一个包含2个神经元的隐藏层(h1和h2)、包含1个神经元的输出层o1。
隐藏层是夹在输入输入层和输出层之间的部分,一个神经网络可以有多个隐藏层。
把神经元的输入向前传递获得输出的过程称为前馈(feedforward)。
我们假设上面的网络里所有神经元都具有相同的权重
w
=
[
0
,
1
]
{w=[0,1]}
w=[0,1]和偏置
b
=
0
{b=0}
b=0,激活函数都是
s
i
g
m
o
i
d
{sigmoid}
sigmoid,那么我们会得到什么输出呢?
h
1
=
h
2
=
f
(
w
∗
x
+
b
)
=
f
(
(
0
∗
2
)
+
(
1
∗
3
)
+
0
)
=
f
(
3
)
=
0.9526
{h_1=h_2=f(w*x+b)=f((0*2)+(1*3)+0)=f(3)=0.9526}
h1=h2=f(w∗x+b)=f((0∗2)+(1∗3)+0)=f(3)=0.9526
o
1
=
f
(
w
∗
[
h
1
,
h
2
]
+
b
)
=
f
(
(
0
∗
h
1
)
+
(
1
∗
h
2
)
+
0
)
=
f
(
0.9526
)
=
0.7216
{o_1=f(w*[h_1,h_2]+b)=f((0*h_1)+(1*h_2)+0)=f(0.9526)=0.7216}
o1=f(w∗[h1,h2]+b)=f((0∗h1)+(1∗h2)+0)=f(0.9526)=0.7216
以下是实现代码:
class OurNeuralNetworks():
"""
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
Each neural has the same weights and bias:
- w = [0, 1]
- b = 0
"""
def __init__(self):
weights = np.array([0, 1])
bias = 0
# The Neuron class here is from the previous section
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# The inputs for o1 are the outputs from h1 and h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetworks()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
训练神经网络
现在我们已经学会了如何搭建神经网络,现在再来学习如何训练它,其实这是一个优化的过程。
假设有一个数据集,包含4个人的身高、体重和性别:
| Name | Weight (lb) | Height (in) | Gender |
|---|---|---|---|
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
现在我们的目标是训练一个网络,根据体重和身高来推测某人的性别。
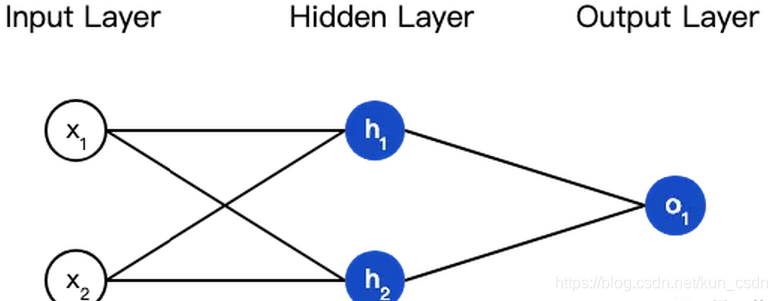
为了简便起见,我们将每个人的身高、体重减去一个固定数值,把性别男定义为1、性别女定义为0。
| Name | Weight (减去135) | Height (减去66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 0 |
| Bob | 25 | 6 | 1 |
| Charlie | 17 | 4 | 1 |
| Diana | -15 | -6 | 0 |
在训练神经网络之前,我们需要有一个标准定义它到底好不好,以便我们进行改进,这就是损失(loss)。
比如用均方误差(MSE)来定义损失:
M
S
E
=
1
n
∑
i
=
1
n
(
y
t
r
u
e
−
y
p
r
e
d
)
2
{MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{true}-y_{pred})^2}
MSE=n1∑i=1n(ytrue−ypred)2
n
{n}
n是样本的数量,在上面的数据集中是4;
y
{y}
y代表人的性别,男性是1,女性是0;
y
t
r
u
e
{y_{true}}
ytrue是变量的真实值,
y
p
r
e
d
{y_{pred}}
ypred是变量的预测值。
顾名思义,均方误差就是所有数据方差的平均值,我们不妨就把它定义为损失函数。预测结果越好,损失就越低,训练神经网络就是将损失最小化。
如果上面网络的输出一直是0,也就是预测所有人都是男性,那么损失是
| Name | y t r u e {y_{true}} ytrue | y p r e d {y_{pred}} ypred | ( y t r u e − y p r e d ) 2 {(y_{true}-y_{pred})^2} (ytrue−ypred)2 |
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
M S E = 1 4 ( 1 + 0 + 0 + 1 ) = 0.5 {MSE=\frac{1}{4}(1+0+0+1)=0.5} MSE=41(1+0+0+1)=0.5
计算损失函数的代码如下:
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
减少神经网络损失
这个神经网络不够好,还要不断优化,尽量减少损失。我们知道,改变网络的权重和偏置可以影响预测值,但我们应该怎么做呢?
为了简单起见,我们把数据集缩减到只包含Alice一个人的数据。于是损失函数就剩下Alice一个人的方差:
M S E = 1 1 ∑ i = 1 1 ( y t r u e − y p r e d ) 2 = ( y t r u e − y p r e d ) 2 = ( 1 − y p r e d ) 2 {MSE=\frac{1}{1}\sum_{i=1}^{1}(y_{true}-y_{pred})^2=(y_{true}-y_{pred})^2=(1-y_{pred})^2} MSE=11∑i=11(ytrue−ypred)2=(ytrue−ypred)2=(1−ypred)2
预测值是由一系列网络权重和偏置计算出来的:
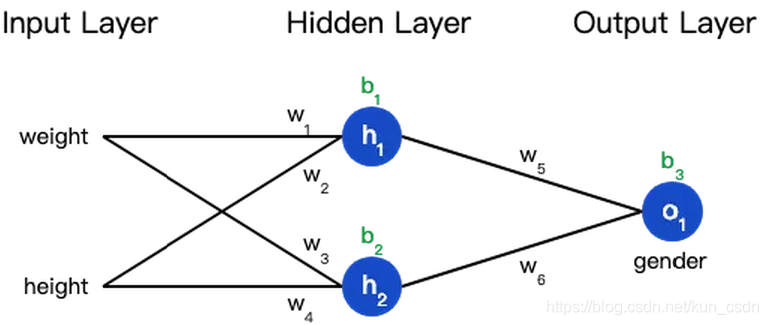
所以损失函数实际上是包含多个权重、偏置的多元函数:
L
(
w
1
,
w
2
,
w
3
,
w
4
,
w
5
,
w
6
,
b
1
,
b
2
,
b
3
)
{L(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b_3)}
L(w1,w2,w3,w4,w5,w6,b1,b2,b3)
(注意!前方高能!需要你有一些基本的多元函数微分知识,比如偏导数、链式求导法则。)
如果调整一下w1,损失函数是会变大还是变小?我们需要知道偏导数∂L/∂w1是正是负才能回答这个问题。
根据链式求导法则:
∂
L
∂
w
1
=
∂
L
∂
y
p
r
e
d
∗
∂
y
p
r
e
d
∂
w
1
{\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}*\frac{\partial y_{pred}}{\partial w_1}}
∂w1∂L=∂ypred∂L∗∂w1∂ypred
可以求得第一项偏导数:
∂
L
∂
y
p
r
e
d
=
∂
(
1
−
y
p
r
e
d
)
2
∂
y
p
r
e
d
=
−
2
(
1
−
y
p
r
e
d
)
{\frac{\partial L}{\partial y_{pred}}=\frac{\partial (1-y_{pred})^2}{\partial y_{pred}}=-2(1-y_{pred})}
∂ypred∂L=∂ypred∂(1−ypred)2=−2(1−ypred)
接下来我们要想办法获得
y
p
r
e
d
{y_{pred}}
ypred和w1的关系,我们已经知道神经元h1、h2和o1的数学运算规则:
y
p
r
e
d
=
o
1
=
f
(
w
5
h
1
+
w
6
h
2
+
b
3
)
{y_{pred}=o_1=f(w_5h_1+w_6h_2+b_3)}
ypred=o1=f(w5h1+w6h2+b3)
实际上只有神经元h1中包含权重w1,所以我们再次运用链式求导法则:
∂
y
p
r
e
d
∂
w
1
=
∂
y
p
r
e
d
∂
h
1
∗
∂
h
1
∂
w
1
{\frac{\partial y_{pred}}{\partial w_1}=\frac{\partial y_{pred}}{\partial h_1}*\frac{\partial h_1}{\partial w_1}}
∂w1∂ypred=∂h1∂ypred∗∂w1∂h1
∂
y
p
r
e
d
∂
h
1
=
w
5
∗
f
′
(
w
5
h
1
+
w
6
h
2
+
h
3
)
{\frac{\partial y_{pred}}{\partial h_1}=w_5*f'(w_5h_1+w_6h_2+h_3)}
∂h1∂ypred=w5∗f′(w5h1+w6h2+h3)
然后求
∂
h
1
∂
w
1
{\frac{\partial h_1}{\partial w_1}}
∂w1∂h1:
h
1
=
f
(
w
1
x
1
+
w
2
x
2
+
b
1
)
{h_1=f(w_1x_1+w_2x_2+b_1)}
h1=f(w1x1+w2x2+b1)
∂
h
1
∂
w
1
=
x
1
∗
f
′
(
w
1
x
1
+
w
2
x
2
+
h
1
)
{\frac{\partial h_1}{\partial w_1}=x_1*f'(w_1x_1+w_2x_2+h_1)}
∂w1∂h1=x1∗f′(w1x1+w2x2+h1)
上面的计算中遇到了2次激活函数
s
i
g
m
o
i
d
{sigmoid}
sigmoid的导数
f
′
(
x
)
{f'(x)}
f′(x),
s
i
g
m
o
i
d
{sigmoid}
sigmoid函数的导数很容易求得:
f
(
x
)
=
1
1
+
e
−
x
{f(x)=\frac{1}{1+e^{-x}}}
f(x)=1+e−x1
f
′
(
x
)
=
e
x
(
1
+
e
−
x
)
2
=
f
(
x
)
∗
(
1
−
f
(
x
)
)
{f'(x)=\frac{e^x}{(1+e^{-x})^2}=f(x)*(1-f(x))}
f′(x)=(1+e−x)2ex=f(x)∗(1−f(x))
总的链式求导公式:
∂
L
∂
w
1
=
∂
L
∂
y
p
r
e
d
∗
∂
y
p
r
e
d
∂
h
1
∗
∂
h
1
∂
w
1
{\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}*\frac{\partial y_{pred}}{\partial h_1}*\frac{\partial h_1}{\partial w_1}}
∂w1∂L=∂ypred∂L∗∂h1∂ypred∗∂w1∂h1
这种向后计算偏导数的系统称为反向传播(backpropagation)。
上面的数学符号太多,下面我们带入实际数值来计算一下。
h
1
、
h
2
和
o
1
{h_1、h_2和o_1}
h1、h2和o1
h
1
=
f
(
x
1
w
1
+
x
2
w
2
+
b
1
)
=
0.0474
{h_1=f(x_1w_1+x_2w_2+b_1)=0.0474}
h1=f(x1w1+x2w2+b1)=0.0474
h
2
=
f
(
x
3
w
3
+
x
4
w
4
+
b
2
)
=
0.0474
{h_2=f(x_3w_3+x_4w_4+b_2)=0.0474}
h2=f(x3w3+x4w4+b2)=0.0474
o
1
=
f
(
h
1
w
5
+
h
2
w
6
+
b
3
)
=
f
(
0.0474
+
0.0474
+
0
)
=
0.524
{o_1=f(h_1w_5+h_2w_6+b_3)=f(0.0474+0.0474+0)=0.524}
o1=f(h1w5+h2w6+b3)=f(0.0474+0.0474+0)=0.524
神经网络的输出y=0.524,没有显示出强烈的是男(1)是女(0)的证据。现在的预测效果还很不好。
∂
L
∂
w
1
=
∂
L
∂
y
p
r
e
d
∗
∂
y
p
r
e
d
∂
h
1
∗
∂
h
1
∂
w
1
{\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}*\frac{\partial y_{pred}}{\partial h_1}*\frac{\partial h_1}{\partial w_1}}
∂w1∂L=∂ypred∂L∗∂h1∂ypred∗∂w1∂h1
- ∂ L ∂ y p r e d = ∂ ( 1 − y p r e d ) 2 ∂ y p r e d = − 2 ( 1 − y p r e d ) = − 2 ( 1 − 0.524 ) = − 0.952 {\frac{\partial L}{\partial y_{pred}}=\frac{\partial (1-y_{pred})^2}{\partial y_{pred}}=-2(1-y_{pred})=-2(1-0.524)=-0.952} ∂ypred∂L=∂ypred∂(1−ypred)2=−2(1−ypred)=−2(1−0.524)=−0.952
- ∂ y p r e d ∂ h 1 = w 5 ∗ f ′ ( w 5 h 1 + w 6 h 2 + h 3 ) = 1 ∗ f ′ ( 0.0474 + 0.0474 + 0 ) = f ( 0.0948 ) ∗ ( 1 − f ( 0.0948 ) ) = 0.249 {\frac{\partial y_{pred}}{\partial h_1}=w_5*f'(w_5h_1+w_6h_2+h_3)=1*f'(0.0474+0.0474+0)=f(0.0948)*(1-f(0.0948))=0.249} ∂h1∂ypred=w5∗f′(w5h1+w6h2+h3)=1∗f′(0.0474+0.0474+0)=f(0.0948)∗(1−f(0.0948))=0.249
- ∂ h 1 ∂ w 1 = x 1 ∗ f ′ ( w 1 x 1 + w 2 x 2 + h 1 ) = − 2 ∗ f ′ ( − 2 + − 1 + 0 ) = − 2 ∗ f ( − 3 ) ∗ ( 1 − f ( − 3 ) ) = − 0.0904 {\frac{\partial h_1}{\partial w_1}=x_1*f'(w_1x_1+w_2x_2+h_1)=-2*f'(-2+-1+0)=-2*f(-3)*(1-f(-3))=-0.0904} ∂w1∂h1=x1∗f′(w1x1+w2x2+h1)=−2∗f′(−2+−1+0)=−2∗f(−3)∗(1−f(−3))=−0.0904
所以 ∂ L ∂ w 1 = − 0.952 ∗ 0.249 ∗ − 0.0904 = 0.0214 {\frac{\partial L}{\partial w_1}=-0.952*0.249*-0.0904 = 0.0214} ∂w1∂L=−0.952∗0.249∗−0.0904=0.0214
这个结果告诉我们:如果增大w1,损失函数L会有一个非常小的增长。
随机梯度下降
下面将使用一种称为随机梯度下降(SGD)的优化算法,来训练网络。
经过前面的运算,我们已经有了训练神经网络所有数据。但是该如何操作?SGD定义了改变权重和偏置的方法:
w
1
←
w
1
−
η
∂
L
∂
w
1
{w_1\leftarrow w_1-\eta \ \frac{\partial L}{\partial w_1}}
w1←w1−η ∂w1∂L
η
{\eta}
η是一个常数,称为学习率(learning rate),它决定了我们训练网络速率的快慢。将
w
1
{w_1}
w1减去
η
∂
L
∂
w
1
{\eta \frac{\partial L}{\partial w_1}}
η∂w1∂L,就等到了新的权重
w
1
{w_1}
w1。
如果我们用这种方法去逐步改变网络的权重
w
{w}
w和偏置
b
{b}
b,损失函数会缓慢地降低,从而改进我们的神经网络。
训练流程如下:
- 从数据集中选择一个样本;
- 计算损失函数对所有权重和偏置的偏导数;
- 使用更新公式更新每个权重和偏置;
- 回到第1步。
Python代码实现这个过程:
def sigmoid(x):
# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork():
"""
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
*** DISCLAIMER ***
The code below is intend to be simple and educational, NOT optimal.
Real neural net code looks nothing like this. Do NOT use this code.
Instead, read/run it to understand how this specific network works.
"""
def __init__(self):
# weights
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# biases
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x is a numpy array with 2 elements, for example [input1, input2]
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
"""
- data is a (n x 2) numpy array, n = # samples in the dataset.
- all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
"""
learn_rate = 0.1
epochs = 1000 # number of times to loop through the entire dataset
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# - - - Do a feedforward (we'll need these values later)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * x[0] + self.w6 * x[1] + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# - - - Calculate partial derivatives.
# - - - Naming: d_L_d_w1 represents "partial L / partial w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Neuron o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Neuron h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Neuron h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# - - - update weights and biases
# Neuron o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# Neuron h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Neuron h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# - - - Calculate total loss at the end of each epoch
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f", (epoch, loss))
# Define dataset
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6] # diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1 # diana
])
# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
随着学习过程的进行,损失函数逐渐减小。
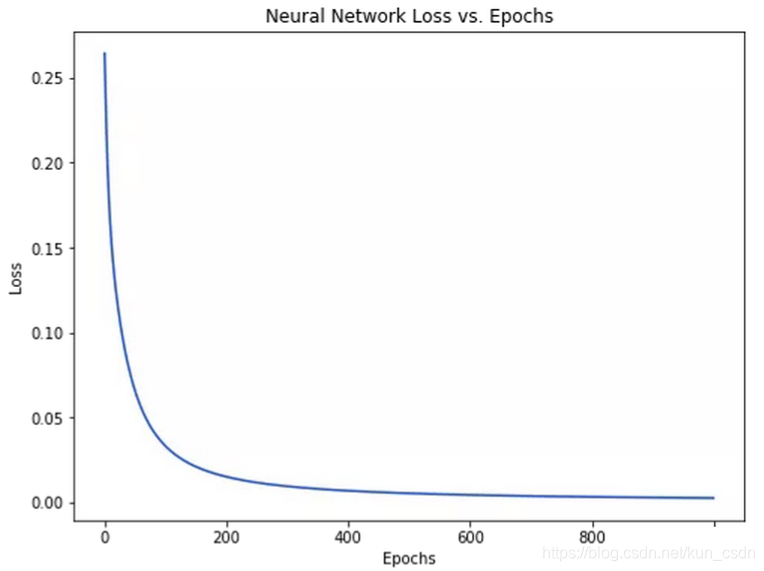
现在我们可以用它来推测出每个人的性别了:
# Make some predictions
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2]) # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)