深度学习 --- 径向基神经网络RBF详解

zsffuture

99350人浏览 · 2018-11-25 12:45:50

zsffuture · 2018-11-25 12:45:50 发布

上一节我们基本上打开了深度学习的大门，其实下一步应该是卷积神经网络即CNN了，但是呢卷积神经网络的最后一层采用的是径向基神经网络，为了以后到CNN不用再费力气将RBF和保持CNN的整体性和连贯性，因此这里我们系统的学习一下，讲解之前我们还是先好好回顾我们的总体学习思路，首先我们从BP神经网络开始，介绍了BP的优缺点和改良思路，后面就开始介绍Hopfield神经网络，该网络是从动力能量角度进行建模的神经网络，但是缺点是存在伪吸引子或者说容易陷入局部最优解，为了解决这个问题我们引入了玻尔兹曼分布和模拟退火算法构成新的神经网络即玻尔兹曼机解决了为伪吸引子的问题，但是带来的问题的是计算量太大，为了解决这个问题，hinton发明了受限玻尔兹曼机，通过吉布斯采样很好的解决了玻尔兹曼机的计算量大的问题，在此基础上，构造了深度置信网络DBN，后面又和BP结合构成DNN即深度学习网络，也因此我们算是打开了深度学习的大门了，后面就是CNN了，这就是我们学习的过程，为了后面的更系统的学习CNN，需要讲解一下径向基神经网络，因为CNN中用到了，好，废话不多说，下面就开始：

径向基基础知识

径向基在机器学习中讲过了一点概念性的东西，不懂的请查看我的这篇博客的后半部分，这里就不细讲了，直接把哪里的结果拿过了。

$\large F(X) = d^p$ $\large p = 1,2,3,.....,P$ $\large \left ( 1 \right )$

采用径向基函数技术解决插值问题的方法是，选择P个基函数个训练数据，各基函数的形式为：
$\large \varphi (\left \| x-x^p \right \|)$ $\large p = 1,2,....,P$ $\large \left ( 2 \right )$
式中，基函数 $\large \varphi$ 为非线性函数，训练数据点 $\large x^p$ 是 $\large \varphi$ 的中心。基函数以输人空间的点x与中心 $\large x^p$ 的距离作为函数的自变量。由于距离是径向同性的，故函数被称为径向基函数。基于径向基函数技术的差值函数定义为基函数的线性组合：

$\large F(x) = \sum_{p=1}^{P}w_p\varphi (\left \| x-x^p \right \|)$ $\large \left ( 3 \right )$

将（1）式的插值条件代入上式，得到P个关于未知系数 $\large w^p$ , $\large p = 1,2,....,P$ 的线性方程组：

$\large \sum_{p=1}^{P}w_p\varphi (\left \| \mathbf{x^1-x^p} \right \|)=d^1$

$\large \sum_{p=1}^{P}w_p\varphi (\left \| \mathbf{x^2-x^p} \right \|)=d^2$

$\large \begin{matrix} \end{matrix}$ $\large \wr$

$\large \sum_{p=1}^{P}w_p\varphi (\left \| \mathbf{x^P-x^p} \right \|)=d^P$ $\large \left ( 4 \right )$

令 $\large \varphi _{ip}=\varphi (\left \|\mathbf{ x^i-x^p} \right \|),i=1,2,...,P,p = 1,2,...,P,$ 则上述方程组可改写为：

$\large \begin{bmatrix} \varphi _{11},\varphi _{12},...,\varphi _{1P} &\\ \varphi _{11},\varphi _{12},...,\varphi _{1P} &\\ ......,......,...,..... &\\ \varphi _{11},\varphi _{12},...,\varphi _{1P} &\\ \end{bmatrix}\begin{bmatrix} w_1 &\\ w_2 &\\ ....&\\ w_P &\\ \end{bmatrix} = \begin{bmatrix} d^1 &\\ d^2 &\\ ....&\\ d^P &\\ \end{bmatrix}$ $\large \left ( 5 \right )$

令 $\large \Phi$ 表示元素 $\large \varphi _{ip}$ 的PxP阶矩阵， $\large w$ 和 $\large d$ 分别表示系数向量和期望输出向量，（5）式还可以写成下面的向量形式：

$\large \Phi w =d$ $\large \left ( 6 \right )$

式中， $\large \Phi$ 称为插值矩阵，若 $\large \Phi$ 为可逆矩阵，就可以从（6）式中解出系数向量 $\large w$ ，即：

$\large w = \Phi ^{-1}d$ $\large \left ( 7 \right )$

高斯径向基函数：

$\large \varphi (r) = e^{-\frac{r^2}{2\delta ^2}}$ $\large \left ( 8 \right )$

横轴就是到中心的距离用半径r表示，如上图，我们发现当距离等于0时，径向基函数等于1，距离越远衰减越快，其中高斯径向基的参数 $\large \delta$ 在支持向量机中被称为到达率或者说函数跌落到零的速度。红色 $\large \delta$ =1，蓝色 $\large \delta$ =5，绿色 $\large \delta$ =0.5，我们发现到达率越小其越窄。

正则化径向基神经网络

正则化RBF网络的结构如下图所示。其特点是：网络具有N个输人节点，P个隐节点，i个输出节点；网络的隐节点数等于输人样本数，隐节点的激活函数常高斯径向基函数，并将所有输人样本设为径向基函数的中心，各径向基函数取统一的扩展常数。

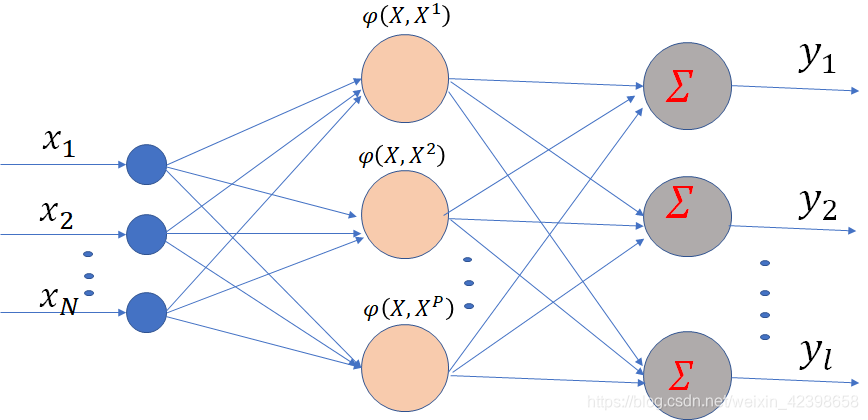
设输入层的任意节点你用i表示，隐节点任一节点用j表示，输出层的任一节点用k表示。对各层的数学描述如下：

输入向量：

$\large \mathbf{x} = (x_1,x_2,...,x_N)^T$

任一隐节点的激活函数：

$\large \varphi _j(\mathbf{x}) , (j = 1,2,3,..,P)$

称为基函数。一般使用高斯函数。

输出权矩阵： $\large w$ ，其中 $\large w_{ik} , (j=1,2,...,P,k=1,2,...,l)$ 为隐层的第j个节点与输出层第k个节点间的突触权值。

输出向量： $\large Y = (y_1,y_2,...,y_l)$

输出层神经元采用线性激活函数。

当输人训练集中的某个样本 $\large \mathbf{x}^p$ 时，对应的期望输出 $\large \mathbf{d}^p$ 就是教师信号。为了确定网络隐层到输出层之间的P个权值，需要将训练集中的样本逐一输人一遍，从而可得到式（4)中的方程组。网络的权值确定后，对训练集的样本实现了完全内插，即对所有样本误差为0。而对非训练集的输人模式，网络的输出值相当于函数的内插，因此径向基函数网络可用作数逼近。
正则化RBF网络具有以下3个特点：
① 正则化网络是一种通用逼近器，只有要足够的节点，它可以以任意精度逼近紧集上的任意多元连续函数。
② 具有最佳逼近特性，即任给一个未知的非线性函数 $\large f$ ，总可以找到一组权值使得正则化网络对于 $\large f$ 的逼近优于所有其可能的选择。

③ 正则化网络得到的解是最佳的，所谓“最佳”体现在同时满足对样本的逼近误差和逼近曲线的平滑性。

正则化RBF网络的学习算法

当采用正则化RBP网络结构时，隐节点数即样本数，基函数的数据中心即为样本本身，只需考虑扩展常数和输出节点的权值。径向基函数的扩展常数可根据数据中心的散布而确定，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为：

$\large \delta = \frac{d_{max}}{\sqrt{2P}}$ $\large \left ( 9 \right )$

式中， $\large d_{max}$ 是样本之间的最大距离；P是样本的数目。

输出层的权值采用最小均方误差算法LMS（不懂的请看这篇文章），LMS的输入向量即为隐节点的输出向量，权值调整公式为：

$\large \Delta\textb{W_K} = \eta (d_k - \mathbf{w_k^T\Phi })\Phi$ $\large \left ( 10 \right )$

$\large \Delta W_k$ 的各分量为：

$\large \Delta\textb{W_{jk}} = \eta (d_k - \mathbf{w_k^T\Phi })\varphi _j$ $\large (j=1,2,...,P,k=1,2,...,l)$ $\large \left ( 11 \right )$

权值初始化任意值。

总结：

正则化的RBF要求所有样本对应一个隐层神经元，所带来额问题是计算量很大，因为一旦样本成千上万则计算量急剧增加，样本量很大带来的另外一个问题是容易达到病态方程组问题，什么是病态方程组问题？当方程组很多时，如样本的不是很精确，稍微有点偏差都会引起权值的剧烈变化，因为样本很多，那么方程组就可能存在多重共线性问题，在岭回归详细探讨了多重共线性问题（有兴趣的可以参考我的这篇文章），因此需要改进RBF神经网络。因此广义的RBF神经网络

广义的RBF神经网络

由于正则化网络的训练样本与“基函数”是一一对应的。当样本数P很大时，实现网络的计算量将大得惊人，此外P很大则权值矩阵也很大，求解网络的权值时容易产生病态问题(illconditioning)。为解决这一问题，可减少隐节点的个数，即N<M<P，N为样本维数，P为样本个数，从而得到广义RBE网络。
广义RBF网络的基本思想是：用径向基函数作为隐单元的“基”，构成隐含层空间。隐含层对输人向量进行变换，将低维空间的模式变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。

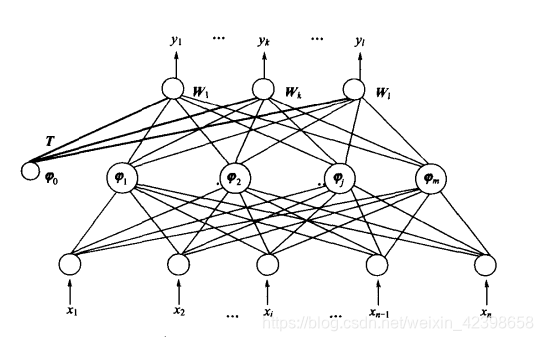
如上图N-M-L结构的广义RBF神经网络结构图，即网络具有N个输入节点，M个隐节点，l个输出节点，且M<P.。这里和上面一样，先从符号解释开始：

输入向量：

$\large \mathbf{x} = (x_1,x_2,...,x_N)^T$

激活函数：

$\large \varphi _j(\mathbf{x}) , (j = 1,2,3,..,P)$ 为任一节点的基函数

一般选用格林函数

输出权矩阵：

$\large w$ ，其中 $\large w_{ik} , (j=1,2,...,P,k=1,2,...,l)$ 为隐层的第j个节点与输出层第k个节点间的突触权值。

输出阈值向量： $\large T = (\mathrm{T_1,T_2,...,T_l})$

网络输出： $\large Y = (y_1,y_2,...,y_l)$

与正则化RBF网络相比，广义RBF网络有以下几点不同：
① 径向基函数的个数M与样本的个数P不相等，且M常常远小于P。
② 径向基函数的中心不再限制在数据点上，而是由训练算法确定。
③ 各径向基数的扩展常数不再统一，其值由训练算法确定。
④ 输出函数的线性中包含阈值参数，用于补偿基函数在样本集上的平均值与目标值之间的差别。

广义RBF网络设计方法

广义RBP网络的设计包括结构设计和参数设计。结构设计主要解决如何确定网络隐节点数的问题，参数设计一般需考虑包括三种参数：各基函数的数据中心和扩展常数，以及输出节点的权值。
根据数据中心的取值方法，广义RBF网的设计方法可分为两类：
（1)第一类方法：数据中心从样本输人中选取一般来说，样本密集的地方中心点可以适当多些，样本稀疏的地方中心点可以少些；若数据本身是均匀分布的，中心点也可以均匀分布。总之，选出的数据中心应具有代表性。径向基函数的扩展常数是根据数据中心的散布而确定的，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为：
$\large \delta = \frac{d_{max}}{\sqrt{2M}}$

式中， $\large d_{max}$ 是所选数据中心之间的最大距离；M是数据中心的数目。
（2）第二类方法：数据中心的自组织选择常采用各种动态聚类算法对数据中心进行自组织选择，在学习过程中需对数据中心的位置进行动态调节，常用的方法是K-means聚类(不懂的建议自行学习一下)，其优点是能根据各聚类中心之间的距离确定各隐节点的扩展常数。由于RBF网的隐节点数对其泛化能力有极大的影响，所以寻找能确定聚类数目的合理方法，是聚类方法设计RBE
网时需首先解决的问题。除聚类算法外，还有梯度训练方法、资源分配网络（RAN)等。

广义RBF网络数据中心的聚类算法

这里默认大家都知道一些简单的聚类思想了，例如最常见的K-means聚类算法原理大家应该理解，这里简单的解释一下K-means的原理，很简单，在数据中我随意选择k个中心点，然后这以这个k个中心数据为基础计算其他数据到此中心的距离，把新数据加入最近的那个中心点，没加入一个数据就计算平均距离然后以这个平均距离作为本类的新中心，继续计算下去，知道数据分类完成了。不懂的建议学习一下。

1989年，Moody和Darken提出一种由两个阶段组成的混合学习过程的思路。第一阶段常采用Duda和Hart1973年提出的K-means聚类算法，其任务是用自组织聚类方法为隐层节点的径向基函数确定合适的数据中心，并根据各中心之间的距离确定隐节点的扩展常数。第二阶段为监督学习阶段，其任务是用有监督学习算法训练输出层权值，一般采用梯度法进行训练。在聚类确定数据中心的位置之前，需要先估计中心的个数M（从而确定了隐节点数），一般需要通过试验来决定。

通过聚类得到径向基的中心后，后面就是确定径向基函数额扩展函数。扩展常数的确定是通过k个聚类中心点的距离决定的，一般去k个中心点彼此距离最小的那个值加入为d， $\large \delta = \lambda d$ 。

利用K-means聚类算法得到各径向基函数的中心和扩展常数后，混合学习过程的第2步是用有监督学习算法得到输出层的权值，常采用LMS法。更简捷的方法是用伪逆法直接计算。以单输出RBF网络为例，设输人为时，第j个隐节点的输出为:

$\large \varphi _{pj} = \varphi (\left \| \mathbf{x^p-c_j} \right \|)$ , $\large p = 1,2,3...,P, j=1,2,3,...,M$
则隐层输出矩阵为：

$\large \hat{\Phi } = [\varphi _{pj}]_{P\times M}$

若RBF网络的待定输出权值为： $\large \mathbf{W} = [w_1,w_2,....,w_M]$ ，则网络输出向量为：

$\large F(X) = \hat{\Phi }w$

令网络输出向量等于期望信号 $\large d$ 。则 $\large w$ 可以用 $\large \hat{\Phi }$ 的伪逆 $\large \hat{\Phi }^+$ 求出：

$\large w = \hat{\Phi }^+d$

$\large \hat{\Phi }^+ = (\hat{\Phi }^T\hat{\Phi })^{-1}\hat{\Phi }^T$

以上就是权值更新思想。下面对比一下RBF和BP的差别：

RBF网络与BP网络都是非线性多层前向网络，它们都是通用逼近器。对于任一个BP网络，总存在一个RBF网络可以代替它，反之亦然。但是，这两个网络也存在着很多不同点：

① RBF网络只有一个隐层，而BP网络的隐层可以是一层也可以是多层的。
② BP网络的隐层和输出层其神经元模型是一样的；而RBF网络的隐层神经元和输出层神经元不仅模型不同，而且在网络中起到的作用也不一样。
③ RBF网络的隐层是非线性的，输出层是线性的。然而，当用BP网络解决模式分类问题时，它的隐层和输出层通常选为非线性的。当用BP网络解决非线性回归问题时，通常选择线性输出层。
④ RBF网络的基函数计算的是输人向量和中心的欧氏距离，而BP网络喼单元的激励函数计算的是输人单元和连接权值间的内积。
⑤ RBF网络使用局部指数衰减的非线性数（如高斯函数）对非线性输人输出映射进行局部逼近。BP网络的隐节点采用输人模式与权向量的内积作为激活函数的自变量，而激活函数则采用Sigmoid函数或硬限幅函数，因此BP网络是对非线性映射的全局逼近。RBF网最显著的特点是隐节点采用输人模式与中心向量的距离（如欧氏距离）作为函数的自变量，并使用径向基函数（如函数）作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性，而且神经元的输人离该中心点越远，神经元的激活程度就越低。隐节点的这个特性常被称为“局部特性”。
由于RBF网络能够逼近任意的非线性函数，可以处理系统内在的难以解析的规律性，并且具有很快的学习收敛速度，因此RBF网络有较为广泛的应用。RBE网络已成功地用于非线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。

以上就是径向基的基本内容了，好本节结束，下一节进入很火的神经网络CNN即卷积神经网络。