本篇博客主要是自己对论文的一些解读以及参考一些博客后的理解，如若有不对之处，请各位道友指出。多谢！

2015年刚提出ResNet的Paper
2016对ResNet进行改进之后的Paper

什么是ResNet

ResNet是一种残差网络，咱们可以把它理解为一个子网络，这个子网络经过堆叠可以构成一个很深的网络。咱们可以先简单看一下ResNet的结构，之后会对它的结构进行详细介绍。

那么可能会有小伙伴疑问，干嘛非要构建这么一个网络来堆叠出一个深层网络呢？干嘛不直接用卷积层对网络进行一个堆叠呢？

为什么要引入ResNet？

我们知道，网络越深，咱们能获取的信息越多，而且特征也越丰富。但是根据实验表明，随着网络的加深，优化效果反而越差，测试数据和训练数据的准确率反而降低了。这是由于网络的加深会造成梯度爆炸和梯度消失的问题。

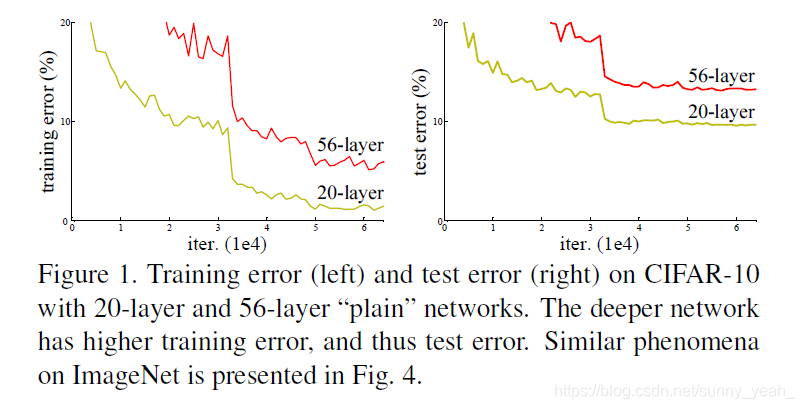
目前针对这种现象已经有了解决的方法：对输入数据和中间层的数据进行归一化操作，这种方法可以保证网络在反向传播中采用随机梯度下降（SGD），从而让网络达到收敛。但是，这个方法仅对几十层的网络有用，当网络再往深处走的时候，这种方法就无用武之地了。

为了让更深的网络也能训练出好的效果，何凯明大神提出了一个新的网络结构——ResNet。这个网络结构的想法主要源于VLAD（残差的想法来源）和Highway Network（跳跃连接的想法来源）。

ResNet详细解说

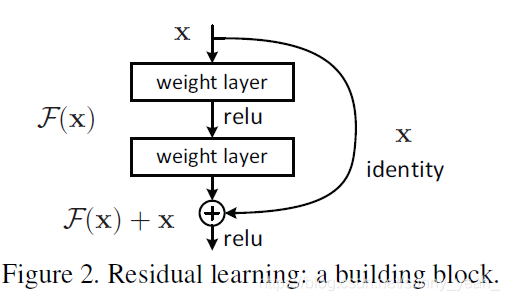
再放一遍ResNet结构图。要知道咱们要介绍的核心就是这个图啦！（ResNet block有两种，一种两层结构，一种三层结构）

咱们要求解的映射为：H(x)
现在咱们将这个问题转换为求解网络的残差映射函数，也就是F(x)，其中F(x) = H(x)-x。

残差：观测值与估计值之间的差。
这里H(x)就是观测值，x就是估计值（也就是上一层ResNet输出的特征映射）。
我们一般称x为identity Function，它是一个跳跃连接；称F(x)为ResNet Function。

那么咱们要求解的问题变成了H(x) = F(x)+x。

有小伙伴可能会疑惑，咱们干嘛非要经过F(x)之后在求解H(x)啊！整这么麻烦干嘛！
咱们开始看图说话：如果是采用一般的卷积神经网络的化，原先咱们要求解的是H(x) = F(x)这个值对不？那么，我们现在假设，在我的网络达到某一个深度的时候，咱们的网络已经达到最优状态了，也就是说，此时的错误率是最低的时候，再往下加深网络的化就会出现退化问题（错误率上升的问题）。咱们现在要更新下一层网络的权值就会变得很麻烦，权值得是一个让下一层网络同样也是最优状态才行。对吧？
但是采用残差网络就能很好的解决这个问题。还是假设当前网络的深度能够使得错误率最低，如果继续增加咱们的ResNet，为了保证下一层的网络状态仍然是最优状态，咱们只需要把令F(x)=0就好啦！因为x是当前输出的最优解，为了让它成为下一层的最优解也就是希望咱们的输出H(x)=x的话，是不是只要让F(x)=0就行了？
当然上面提到的只是理想情况，咱们在真实测试的时候x肯定是很难达到最优的，但是总会有那么一个时刻它能够无限接近最优解。采用ResNet的话，也只用小小的更新F(x)部分的权重值就行啦！不用像一般的卷积层一样大动干戈！

现在大家已经理解了为啥只要用F(x)+x来表示H(x)了吧！
它的公式也相当简单（这里给出两层结构的）：a^[l+2]=Relu(W^[l+2](Relu(W^[l+1]a^[l]+b^[l+1])+b^[l+2]+a^[l])
（不理解这个公式的小伙伴可以跳到我之前关于BP的博客瞅瞅：BP——反向传播算法详解及代码）

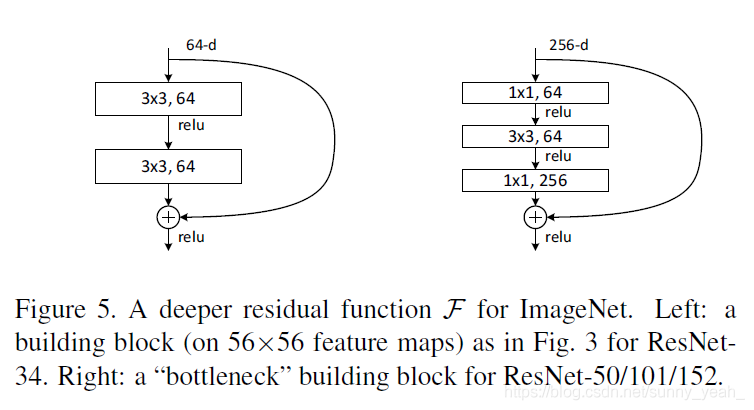
注意：如果残差映射(F(x))的结果的维度与跳跃连接(x)的维度不同，那咱们是没有办法对它们两个进行相加操作的，必须对x进行升维操作，让他俩的维度相同时才能计算。
升维的方法有两种：

• 全0填充；
• 采用1*1卷积。

最后的实验结果表明，ResNet在上百层都有很好的表现，但是当达到上千层了之后仍然会出现退化现象。不过在2016年的Paper中对ResNet的网络结构进行了调整，使得当网络达到上千层的时候仍然具有很好的表现。有兴趣的小伙伴可以自己瞅瞅论文。

做完汇报之后，老师向我提出了一个问题，不知道有没有童鞋知道答案：
1.既然采用了残差结构，为什么当层数达到10³的数量级时，会出现退化问题？
【果然我还没有真正参透ResNet】

我相中的两篇相关博客推荐给大家：
[1]残差网络ResNet笔记
[2]ResNet介绍-上善若水