无人驾驶汽车系统入门(六)——基于传统计算机视觉的车道线检测(1)
无人驾驶汽车系统入门(六)——基于传统计算机视觉的车道线检测(1)感知,作为无人驾驶汽车系统中的“眼睛”,是目前无人驾驶汽车量产和商用化的最大障碍之一(技术角度),目前,高等级的无人驾驶汽车系统仍然非常依赖于激光雷达的测量,通过激光雷达构造周围环境的3D地图,从而为无人驾驶系统的决策和规划提供准确的环境信息和自身相对的位置信息。然而,激光雷达雷达在成本,解析度的方面都不理想,所以基于视
无人驾驶汽车系统入门(六)——基于传统计算机视觉的车道线检测(1)
感知,作为无人驾驶汽车系统中的“眼睛”,是目前无人驾驶汽车量产和商用化的最大障碍之一(技术角度),
目前,高等级的无人驾驶汽车系统仍然非常依赖于激光雷达的测量,通过激光雷达构造周围环境的3D地图,从而为无人驾驶系统的决策和规划提供准确的环境信息和自身相对的位置信息。然而,激光雷达雷达在成本,解析度的方面都不理想,所以基于视觉的无人驾驶相关技术(主要在感知方面)近几年发展迅猛,本节我们从传统的 计算机视觉(Computer Version, CV) 出发,来了解并且实践基于传统计算机视觉算法的车道线检测技术。
原创不易,转载请注明出处:http://blog.csdn.net/adamshan/article/details/78712120
视觉感知VS激光雷达
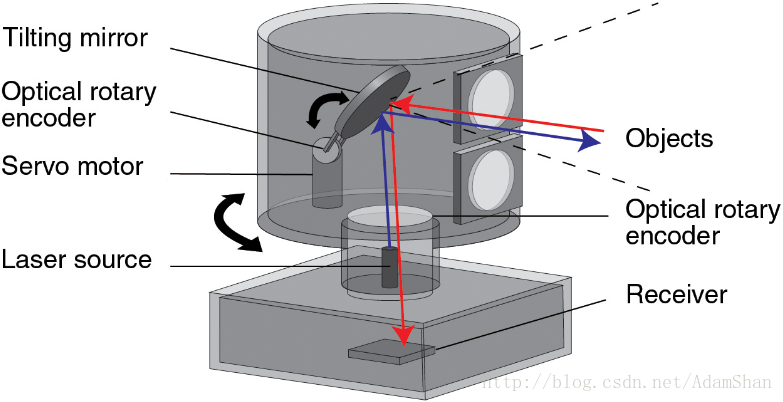
激光雷达能够为无人驾驶汽车提供障碍物检测,高精度地图和定位等多方面的支持,在目前各个研究团队广泛使用。下图是激光雷达的简易构造:
激光雷达以一定的角速度旋转,发射出波长在600nm到1000nm之间的激光射线,同时收集来自反射点的信息,激光雷达每旋转一周,收集到的反射点的坐标构成的一个集合,我们称之为 点云(Point Cloud)。下图就是一张点云图:
激光雷达具有可靠性高,障碍物细节分辨以及精准测距等优点,同时不受光线条件的影响。但是,激光雷达的价格居高不下,例如目前在各个研究团队中广泛使用的Velodyne HDL-64E 激光雷达的售价就在10万美元左右,这使得成本成为搭载激光雷达的无人驾驶汽车的商用化的障碍。
作为比较,基于计算机视觉(Computer Version, CV)的感知成本相对低,结合视觉,IMU+GPS以及毫米波雷达的方案是目前已经商用驾驶辅助系统中采用的主流方案(例如特斯拉的Autopilot),计算机视觉是指 通过图像来感知和理解我们的世界 的科学。对于无人驾驶而言,计算机视觉可以帮助确定车道线的位置,识别车辆,行人以及其他事物,以确保无人车的形式安全,基于深度学习的技术,我们甚至可以实现端到端的自动驾驶(输入图像,输出操作)。
此外,人类驾驶员在做感知的时候只需要一双眼睛(偶尔可能需要用耳朵去听声音),而不需要精确知道距离障碍物有多少厘米,障碍物长宽高分别是多少厘米等,所以我们可以相信——无人驾驶的最终形态或许就像人类驾驶一样仅仅需要视觉感知。
本节我们将使用传统的计算机视觉技术进行车道线的检测,同时基于检测出来的车道线计算车道线的曲率和车辆偏离车道线中心线的距离。在下一届中,我们将使用TensorFlow实现基于深度学习的车道线检测。
相机标定
相机标定(Camera Calibration) 通常是做计算机视觉的第一步,首先,为什么要做相机标定呢?因为我们通过相机镜头记录下的图像往往存在一定程度的失真,这种失真往往表现为 图像畸变(Image Distortion) 。畸变分为两类:
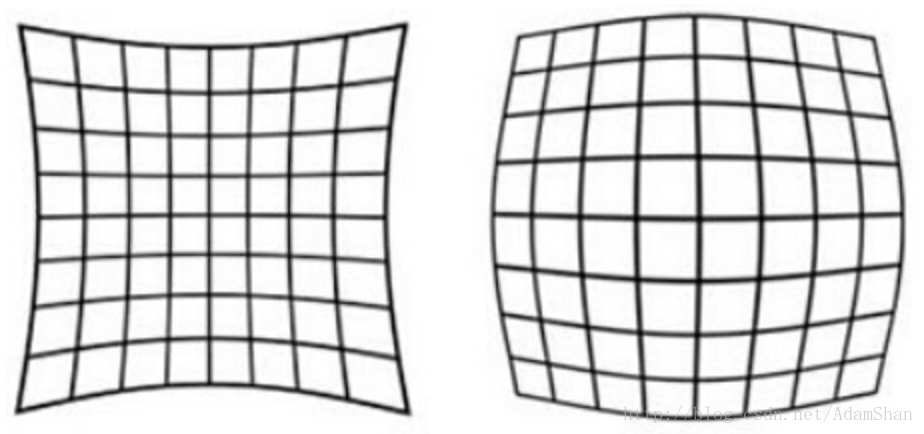
- 径向畸变(radial distortion):由于透镜的特性,光线容易在相机镜头的边缘出现较小或者较大幅度的弯曲,称之为径向畸变。这种畸变在普通廉价的镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图:
- 切向畸变(tangential distortion):是由于透镜本身与相机传感器平面(成像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。
畸变(distortion) 是对直线投影(rectilinear projection)的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变(optical aberration)。可能由于摄像机镜头的原因,这里不讨论,有兴趣的可以查阅光学畸变的相关的资料。
即便一般能够由五个参数来采集,我们称之为 畸变参数(distortion parameters) ,我们使用 D=(k1,k2,p1,p2,k3) <script type="math/tex" id="MathJax-Element-125">D = (k_1, k_2, p_1, p_2, k_3)</script> 来表示,对于径向畸变,可以使用如下公式进行矫正:
对于切向畸变,可以用如下公式来矫正:
以上公式中:
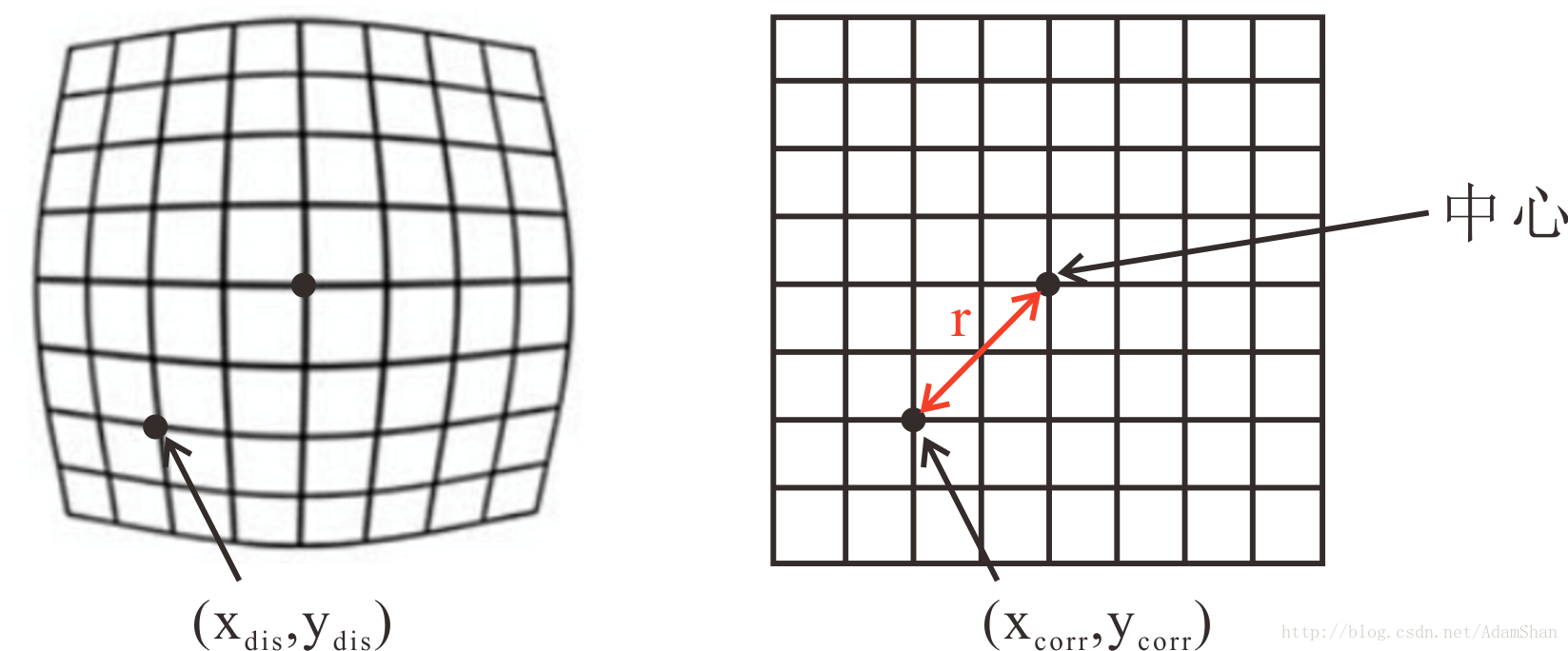
- xdis <script type="math/tex" id="MathJax-Element-110">x_{dis}</script> 和 ydis <script type="math/tex" id="MathJax-Element-111">y_{dis}</script> 表示有畸变的坐标;
- xcorr <script type="math/tex" id="MathJax-Element-112">x_{corr}</script> 和 ycorr <script type="math/tex" id="MathJax-Element-113">y_{corr}</script> 表示修复后的坐标;
- k1 <script type="math/tex" id="MathJax-Element-114">k_1</script> , k2 <script type="math/tex" id="MathJax-Element-115">k_2</script> , k3 <script type="math/tex" id="MathJax-Element-116">k_3</script> 表示径向畸变参数;
- p1 <script type="math/tex" id="MathJax-Element-117">p_1</script> , p2 <script type="math/tex" id="MathJax-Element-118">p_2</script> 表示切向畸变参数;
- r <script type="math/tex" id="MathJax-Element-119">r</script> 表示矫正以后的坐标到图片中心的距离
直接看公式难以理解,我们看如下的图像:
这就是为什么我们标定相机通常使用棋盘图像了,下面我们使用OpenCV来实现一下相机标定。
相机,棋盘图
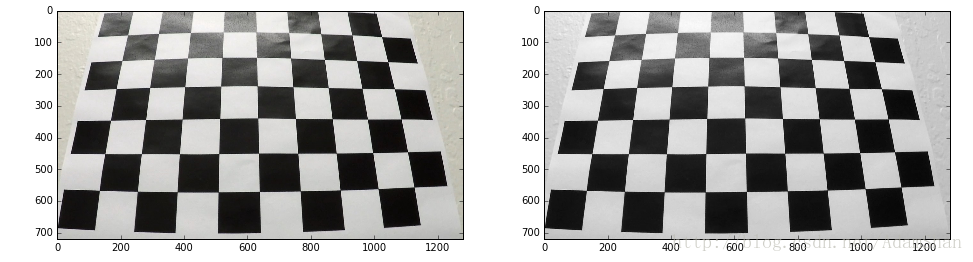
首先从各个角度对这个棋盘拍照,得到一系列如下的照片:
一般来说,使用相机在各个角度拍摄20张左右的棋盘图即可完成后面的标定工作。
使用OpenCV找出棋盘的对角点
首先读取图像并转为灰度图:
from __future__ import print_function
import numpy as np
import cv2
import matplotlib.pyplot as plt
import pickle
%matplotlib inline
cal = plt.imread('calibration1.jpg')
fig1 = plt.figure(1, figsize=(16, 9))
cal_gray = cv2.cvtColor(cal, cv2.COLOR_RGB2GRAY)
plt.subplot(2,2,1)
plt.imshow(cal)
plt.subplot(2,2,2)
plt.imshow(cal_gray, cmap='gray')使用OpenCV的cv2.findChessboardCorners()函数找出棋盘图中的对角(即图片中黑白相对的点的坐标),同时使用cv2.drawChessboardCorners()将之画出来:
ret, corners = cv2.findChessboardCorners(cal_gray, (9, 6),None)
if ret == True:
cal = cv2.drawChessboardCorners(cal, (9, 6), corners, ret)
plt.imshow(cal)在上图中我们查找出了这个棋盘图内
objp = np.zeros((6*9, 3), np.float32)
objp[:, :2] = np.mgrid[0:9, 0:6].T.reshape(-1, 2)
img_points = []
obj_points = []
img_points.append(corners)
obj_points.append(objp)对所有的的标定用的棋盘图像都进行上述操作求得对角的像素位置和实际相对位置(对于一个棋盘来说,实际相对位置其实恒定的),并将这些都添加到 img_points 和 obj_points 两个列表中。最后我们使用OpenCV中的 cv2.calibrateCamera() 即可求得这个相机的畸变系数,在后面的所有图像的矫正都可以使用这一组系数来完成。
image_size = (cal.shape[1], cal.shape[0])
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points,
image_size, None, None)矫正一张图像我们使用 cv2.undistort() 方法来实现:
# Read in a test image
img = cv2.imread('calibration3.jpg')
undist = cv2.undistort(img, mtx, dist, None, mtx)
plt.subplot(2,2,1)
plt.imshow(img)
plt.subplot(2,2,2)
plt.imshow(undist)矫正的结果:
我们发现经过标定以后,相机拍出来的图像更接近于真实情况,因失真造成的”扭曲的直线”也被纠正过来。
确定ROI
ROI(Region of interest) 即我们处理一个视觉任务时“感兴趣的区域”,当然不同的任务ROI是不一样的,对于车道线检测而言(如下图),ROI就是车辆的前方的车道线区域:
我们可以通过透视变换来获得一个相对更加直观的视角(比如说在天空俯视的视角),然后在新的视角来圈出ROI。 透视变换(Perspective Transformation) 是将图片投影到一个新的 视平面(Viewing Plane) ,也称作 投影映射(Projective Mapping) 。在OpenCV中,通过使用函数 cv2.getPerspectiveTransform() 和 cv2.warpPerspective() 即可完成对一张图片的透视变换。
透视变换基于给定的映射关系,通过对原图像进行扭曲,从而得到一个近似另一个视角的图像
首先我们读取并且矫正图像,矫正后的结果:
对直道进行透视变换:
def perspective_transform(img, M):
img_size = (img.shape[1], img.shape[0])
warped = cv2.warpPerspective(img, M, img_size, flags=cv2.INTER_LINEAR)
return warped
# left_top to left_bottom,
corners = [(603, 445), (677, 445), (1105, 720), (205, 720)]
wrap_offset = 150
src_corners = [(603, 445), (677, 445), (1105, 720), (205, 720)]
dst_corners = [(205 + wrap_offset, 0), (1105 - wrap_offset, 0), (1105 - wrap_offset, 720), (205 + wrap_offset, 720)]
M = cv2.getPerspectiveTransform(np.float32(src_corners), np.float32(dst_corners))
wrap_img= perspective_transform(straight_lines1, M)
subplot(1, 2, [straight_lines1, wrap_img])结果如图:
我们解读一下代码:cv2.getPerspectiveTransform() 需要两个参数 src 和 dst,他们分别为原图像中能够表示一个矩形的四个点的坐标以及扭曲以后图像的边缘四角在当前图像中的坐标,这两个矩形的坐标不同的相机的数值也不同,不如说实例中相机的分辨率为 1280×720 <script type="math/tex" id="MathJax-Element-95">1280 \times 720</script> , 那么 [(603, 445), (677, 445), (1105, 720), (205, 720)] 在图像中构成一个梯形,这个梯形在俯视图(或者说鸟瞰图)中是一个长方形,然后我们以这个梯形的高作为目标图像的高,前后各减去一个偏移(在实例中这个偏移是150个像素),就是我们的目标图像这个目标图像,也即是我们的ROI。
下面我们就可以在这个鸟瞰图上来做道路线检测了,由于篇幅的原因,道路线检测算法以及完整代码都将在下一篇博客中给出,希望大家多关注收藏!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容

















所有评论(0)