本文作者注：

OpenCV使用方法

flann::Index flannIndex(descriptors_1,flann::LshIndexParams(12,20,2),cvflann::FLANN_DIST_HAMMING);
Mat matchIndex(descriptors_2.rows,2,CV_32SC1),matchDistance(descriptors_2.rows,2,CV_32SC1);
flannIndex.knnSearch(descriptors_2,matchIndex,matchDistance,2,flann::SearchParams());
vector<DMatch> goodMatches;
for (int i = 0;i<matchDistance.rows;i++)
{
if (matchDistance.at<float>(i,0)<0.6*matchDistance.at<float>(i,1))
{
DMatch dmatch(i,matchIndex.at<int>(i,0),matchDistance.at<float>(i,0));
goodMatches.push_back(dmatch);
}
}
//调用drawMatches方法可以进行绘画
可以看出重要的就是Index这个类的构造，可以使用不同的IndexParams，这在下面也给出了详细的说明。


1.     简介

         在计算机视觉和机器学习中，对于一个高维特征，找到训练数据中的最近邻计算代价是昂贵的。对于高维特征，目前来说最有效的方法是 the randomized k-d forest和the priority search k-means tree，而对于二值特征的匹配 multiple hierarchical clusteringtrees则比LSH方法更加有效。

        目前来说，fast library for approximate nearest neighbors (FLANN)库可以较好地解决这些问题。

2.     快速近似NN匹配（FAST APPROXIMATE NN MATCHING）

2.1 随机k-d树算法（The Randomized k-d TreeAlgorithm）

a. Classick-d tree

        找出数据集中方差最高的维度，利用这个维度的数值将数据划分为两个部分，对每个子集重复相同的过程。

        参考http://www.cnblogs.com/eyeszjwang/articles/2429382.html。

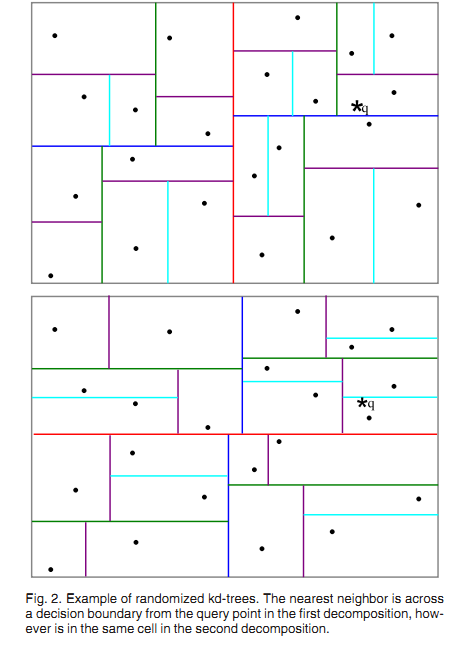
b.  Randomizedk-d tree

        建立多棵随机k-d树，从具有最高方差的N_d维中随机选取若干维度，用来做划分。在对随机k-d森林进行搜索时候，所有的随机k-d树将共享一个优先队列。

       增加树的数量能加快搜索速度，但由于内存负载的问题，树的数量只能控制在一定范围内，比如20，如果超过一定范围，那么搜索速度不会增加甚至会减慢。


2.2  优先搜索k-means树算法（The Priority Search K-MeansTree Algorithm）

        随机k-d森林在许多情形下都很有效，但是对于需要高精度的情形，优先搜索k-means树更加有效。 K-means tree 利用了数据固有的结构信息，它根据数据的所有维度进行聚类，而随机k-d tree一次只利用了一个维度进行划分。

2.2.1  算法描述

算法1 建立优先搜索k-means tree:

(1)  建立一个层次化的k-means 树；

(2)  每个层次的聚类中心，作为树的节点；

(3)  当某个cluster内的点数量小于K时，那么这些数据节点将做为叶子节点。


算法2 在优先搜索k-means tree中进行搜索：

(1)  从根节点N开始检索；

(2)  如果是N叶子节点则将同层次的叶子节点都加入到搜索结果中，count += |N|；

(3)  如果N不是叶子节点，则将它的子节点与query Q比较，找出最近的那个节点Cq，同层次的其他节点加入到优先队列中；

(4)  对Cq节点进行递归搜索；

(5)  如果优先队列不为空且 count<L，那么从取优先队列的第一个元素赋值给N，然后重复步骤(1)。


        聚类的个数K，也称为branching factor 是个非常主要的参数。

        建树的时间复杂度 = O( ndKI ( log(n)/log(K) ))  n为数据点的总个数，I为K-means的迭代次数。搜索的时间复杂度 = O( L/K * Kd * ( log(n)/(log(K) ) ) = O(Ld ( log(n)/(log(K) ) )。

2.3 层次聚类树 （The Hierarchical ClusteringTree）

        层次聚类树采用k-medoids的聚类方法，而不是k-means。即它的聚类中心总是输入数据的某个点，但是在本算法中，并没有像k-medoids聚类算法那样去最小化方差求聚类中心，而是直接从输入数据中随机选取聚类中心点，这样的方法在建立树时更加简单有效，同时又保持多棵树之间的独立性。

        同时建立多棵树，在搜索阶段并行地搜索它们能大大提高搜索性能（归功于随机地选择聚类中心，而不需要多次迭代去获得更好的聚类中心）。建立多棵随机树的方法对k-d tree也十分有效，但对于k-means tree却不适用。

   


FLANN介绍

FLANN库全称是Fast Library for Approximate Nearest Neighbors，它是目前最完整的（近似）最近邻开源库。不但实现了一系列查找算法，还包含了一种自动选取最快算法的机制。

flann::Index_类

该类模板是最近邻索引类，该类用于抽象不同类型的最近邻搜索的索引。 
以下是flann::Index_类的声明：

template <typename T>
class
#ifndef _MSC_VER
 FLANN_DEPRECATED
#endif
 Index_ {
public:
        typedef typename L2<T>::ElementType ElementType;
        typedef typename L2<T>::ResultType DistanceType;

    Index_(const Mat& features, const ::cvflann::IndexParams& params);

    ~Index_();

    void knnSearch(const vector<ElementType>& query, vector<int>& indices, vector<DistanceType>& dists, int knn, const ::cvflann::SearchParams& params);
    void knnSearch(const Mat& queries, Mat& indices, Mat& dists, int knn, const ::cvflann::SearchParams& params);

    int radiusSearch(const vector<ElementType>& query, vector<int>& indices, vector<DistanceType>& dists, DistanceType radius, const ::cvflann::SearchParams& params);
    int radiusSearch(const Mat& query, Mat& indices, Mat& dists, DistanceType radius, const ::cvflann::SearchParams& params);

    void save(std::string filename)
        {
            if (nnIndex_L1) nnIndex_L1->save(filename);
            if (nnIndex_L2) nnIndex_L2->save(filename);
        }

    int veclen() const
    {
            if (nnIndex_L1) return nnIndex_L1->veclen();
            if (nnIndex_L2) return nnIndex_L2->veclen();
        }

    int size() const
    {
            if (nnIndex_L1) return nnIndex_L1->size();
            if (nnIndex_L2) return nnIndex_L2->size();
        }

        ::cvflann::IndexParams getParameters()
        {
            if (nnIndex_L1) return nnIndex_L1->getParameters();
            if (nnIndex_L2) return nnIndex_L2->getParameters();

        }

        FLANN_DEPRECATED const ::cvflann::IndexParams* getIndexParameters()
        {
            if (nnIndex_L1) return nnIndex_L1->getIndexParameters();
            if (nnIndex_L2) return nnIndex_L2->getIndexParameters();
        }

private:
        // providing backwards compatibility for L2 and L1 distances (most common)
        ::cvflann::Index< L2<ElementType> >* nnIndex_L2;
        ::cvflann::Index< L1<ElementType> >* nnIndex_L1;
};

构造函数flann::Index_::Index_

flann::Index_<T>::Index_(const Mat& features, const IndexParams& params)
/*
Parameters: 
features – Matrix of containing the features(points) to index. The size of the matrix is num_features x feature_dimensionality and the data type of the elements in the matrix must coincide with the type of the index.
params – Structure containing the index parameters. The type of index that will be constructed depends on the type of this parameter. See the description.
*/

参数features，是包含用于构建索引的特征的矩阵；参数params，是包含索引参数的结构。 
该构造函数所实例的快速搜索结构是根据参数params所指定的特定算法来构建的。params是由IndexParams的派生类的引用。 
其中： 
* LinearIndexParams，该结构对应的索引进行线性的、暴力(brute-force)的搜索。

  • KDTreeIndexParams，该方法对应的索引结构由一组随机kd树构成(randomized kd-trees)，它可以平行地进行搜索。
struct KDTreeIndexParams : public IndexParams
{
    KDTreeIndexParams( int trees = 4 );
};
//trees:The number of parallel kd-trees to use. Good values are in the range
  • KMeansIndexParams，该方法对应的索引结构是一个层次k均值树(a hierarchical k-means tree)。
struct KMeansIndexParams : public IndexParams
{
    KMeansIndexParams(
        int branching = 32,
        int iterations = 11,
        flann_centers_init_t centers_init = CENTERS_RANDOM,
        float cb_index = 0.2 );
};
  • CompositeIndexParams，该结构结合随机kd树和层次k均值树来构建索引。
struct CompositeIndexParams : public IndexParams
{
    CompositeIndexParams(
        int trees = 4,
        int branching = 32,
        int iterations = 11,
        flann_centers_init_t centers_init = CENTERS_RANDOM,
        float cb_index = 0.2 );
};
  • LshIndexParams，该结构使用multi-probe LSH方法创建索引（Multi-Probe LSH: Efficient Indexing for High-Dimensional Similarity Search by Qin Lv, William Josephson, Zhe Wang, Moses Charikar, Kai Li., Proceedings of the 33rd International Conference on Very Large Data Bases (VLDB). Vienna, Austria. September 2007）。
struct LshIndexParams : public IndexParams
{
    LshIndexParams(
        unsigned int table_number,
        unsigned int key_size,
        unsigned int multi_probe_level );
};
  • AutotunedIndexParams，该结构是根据数据自动选取最优的索引类型来提供最好的性能。
struct AutotunedIndexParams : public IndexParams
{
    AutotunedIndexParams(
        float target_precision = 0.9,
        float build_weight = 0.01,
        float memory_weight = 0,
        float sample_fraction = 0.1 );
};
  • SavedIndexParams，该结构用于加载存放在硬盘的索引结构。
struct SavedIndexParams : public IndexParams
{
    SavedIndexParams( std::string filename );
};
//filename:The filename in which the index was saved.

flann::Index_::knnSearch

根据给定的查询数据，利用构建的索引来执行k近邻搜索。

void flann::Index_<T>::knnSearch(const vector<T>& query, vector<int>& indices, vector<float>& dists, int knn, const SearchParams& params)
void flann::Index_<T>::knnSearch(const Mat& queries, Mat& indices, Mat& dists, int knn, const SearchParams& params)

flann::Index_::radiusSearch

根据给定的查询数据，执行基于半径的最近邻搜索。

int flann::Index_<T>::radiusSearch(const vector<T>& query, vector<int>& indices, vector<float>& dists, float radius, const SearchParams& params)
int flann::Index_<T>::radiusSearch(const Mat& query, Mat& indices, Mat& dists, float radius, const SearchParams& params)

flann::Index_::save

将索引存成文件。

void flann::Index_<T>::save(std::string filename)

flann::Index_::getIndexParameters

得到索引参数。

const IndexParams* flann::Index_<T>::getIndexParameters()

利用FLANN进行特征点匹配

接下来给出一段小的官方示例程序，使用 FlannBasedMatcher 接口以及函数 FLANN 实现快速高效匹配。 
这段代码的主要流程分为以下几部分：

  1. 使用SURF特征提取关键点
  2. 计算SURF特征描述子
  3. 使用FLANN匹配器进行描述子向量匹配

OpenCV中KeyPoint Matching的方法

OpenCV提供了 两种Matching方式 ： 
? Brute-force matcher (cv::BFMatcher) 
? Flann-based matcher (cv::FlannBasedMatcher) 
Brute-force matcher就是用暴力方法找到点集一中每个descriptor在点集二中距离最近的 descriptor； 
Flann-based matcher 使用快速近似最近邻搜索算法寻找。 
为了提高检测速度，你可以调用matching函数前，先训练一个matcher。训练过程可以首先使用cv:: FlannBasedMatcher来优化，为 descriptor建立索引树，这种操作将在匹配大量数据时发挥巨大作用（比如在上百幅图像的数据集中查找匹配图像）。而 Brute-force matcher在这个过程并不进行操作，它只是将train descriptors保存在内存中。

代码示例

#include <stdio.h>
#include <iostream>
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/nonfree/features2d.hpp"

using namespace cv;

/** @function main */
int main( int argc, char** argv )
{
    Mat img_1 = imread("box.png", CV_LOAD_IMAGE_GRAYSCALE );
    Mat img_2 = imread("box_in_scene.png", CV_LOAD_IMAGE_GRAYSCALE );

    if( !img_1.data || !img_2.data )
    { std::cout<< " --(!) Error reading images " << std::endl; return -1; }

    //-- Step 1: Detect the keypoints using SURF Detector
    int minHessian = 400;

    SurfFeatureDetector detector( minHessian );

    std::vector<KeyPoint> keypoints_1, keypoints_2;

    detector.detect( img_1, keypoints_1 );
    detector.detect( img_2, keypoints_2 );

    //-- Step 2: Calculate descriptors (feature vectors)
    SurfDescriptorExtractor extractor;

    Mat descriptors_1, descriptors_2;

    extractor.compute( img_1, keypoints_1, descriptors_1 );
    extractor.compute( img_2, keypoints_2, descriptors_2 );

    //-- Step 3: Matching descriptor vectors using FLANN matcher
    FlannBasedMatcher matcher;
    std::vector< DMatch > matches;
    matcher.match( descriptors_1, descriptors_2, matches );

    double max_dist = 0; double min_dist = 100;

    //-- Quick calculation of max and min distances between keypoints
    for( int i = 0; i < descriptors_1.rows; i++ )
    { double dist = matches[i].distance;
    if( dist < min_dist ) min_dist = dist;
    if( dist > max_dist ) max_dist = dist;
    }

    printf("-- Max dist : %f \n", max_dist );
    printf("-- Min dist : %f \n", min_dist );

    //-- Draw only "good" matches (i.e. whose distance is less than 2*min_dist )
    //-- PS.- radiusMatch can also be used here.
    std::vector< DMatch > good_matches;

    for( int i = 0; i < descriptors_1.rows; i++ )
    { if( matches[i].distance < 2*min_dist )
    { good_matches.push_back( matches[i]); }
    }

    //-- Draw only "good" matches
    Mat img_matches;
    drawMatches( img_1, keypoints_1, img_2, keypoints_2,
        good_matches, img_matches, Scalar::all(-1), Scalar::all(-1),
        vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS );

    //-- Show detected matches
    imshow( "Good Matches", img_matches );

    for( int i = 0; i < good_matches.size(); i++ )
    { printf( "-- Good Match [%d] Keypoint 1: %d  -- Keypoint 2: %d  \n", i, good_matches[i].queryIdx, good_matches[i].trainIdx ); }

    waitKey(0);

    return 0;
}

实验结果

技术分享
技术分享





Logo
百度飞桨AI Studio社区

学大模型，用大模型上飞桨星河社区！每天8点V100G算力免费领！免费领取ERNIE 4.0 100w Token >>>

更多推荐

cover

利用Amazon Bedrock畅玩Claude 3等多种领先模型，抢占AI高地(体验倒计时4小时)

avatar 百度飞桨星河社区
cover

RAPTOR：索引树状 RAG，使用树结构来捕捉文本的高级和低级细节

avatar 百度飞桨星河社区

RAG介绍

LlamaIndex是一个基于大型语言模型（LLM）的应用程序数据框架，旨在连接LLM与外部数据，特别是私有或特定领域的数据，以实现更准确的文本生成和知识增强。

avatar 百度飞桨星河社区