例子如下：
假设数据挖掘的任务是将如下的8个点（用（x，y）代表位置）聚类为3个簇。

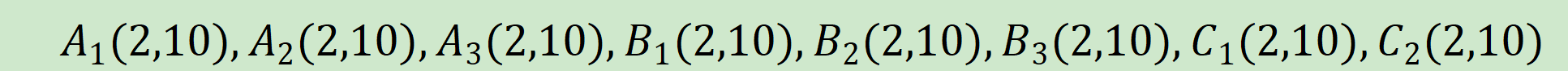
距离是欧氏距离。假设初始我们选择，和分别为每个簇的中心，用k-均值算法给出：
a)在第一轮执行后的3个簇中心
b)最后的三个簇

算法思想：

算法：k-均值。用于划分的k-均值算法，其中每个簇的中心都用簇中所有对象的均值来表示。
输入：
k:簇的数目
D:包含n个对象的数据集
输出：k个簇的集合。
方法：
（1）从D中任意选择k个对象作为初始簇中心；
（2）repeat
（3）根据簇中对象的均值，将每个对象分配到最相似的簇；
（4）更新簇均值，即重新计算每个簇中对象的均值；
（3）until不再发生变化

对于本例：

1）簇的数目k确定为：3；
2）D:数据存储在mydata.xlsx 表格当中；
3）选择第1，4，7位置的点位置作为初始簇中心；
4）距离函数：采用欧式距离

数据放置

1）需要和matlab函数文件放在同一文件夹之下，或者自己改路径
2）取名：mydata.xlsx
3）放在sheet1(创建的表格第一页默认就是这个，不用改)
4）如图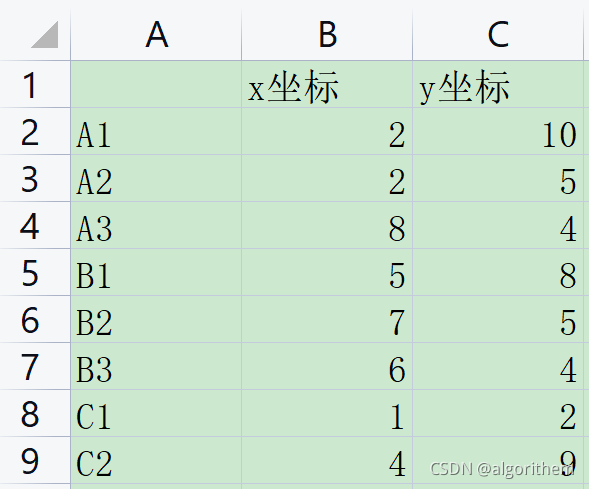

对于问题（a）：

结果及代码如下：

%%
clc; close all; clear
%%数据初始化(x1,y1)
data=xlsread("mydata.xlsx","Sheet1","B2:C9");
 
%%选取的A1，B1,C1作为簇的初始中心
A=data(1,:);
B=data(4,:);
C=data(7,:);
 
%%第一轮执行后的三个簇中心
dis=[];        %距离矩阵
D=[];
label=[];       %每个点的归属，取值1，2，3，分别表示A,B,C
[m,n]=size(data);
for i=1:m
    for j=1:m
        D(i,j)=sqrt((data(i,1)-data(j,1))^2+(data(i,2)-data(j,2))^2);
    end
end
dis=[D(1,:);D(4,:);D(7,:)];
[~,order]=sort(dis);
label=order(1,:);
    %%新的簇中心
    center1=[];
    center2=[];
    center3=[];
    for i=1:m
        if label(i)==1
            center1=[center1;data(i,:)];
        end
        if label(i)==2
            center2=[center2;data(i,:)];
        end
        if label(i)==3
            center3=[center3;data(i,:)];
        end
    end
    A=mean(center1,1);
    B=mean(center2,1);
    C=mean(center3,1);
 
%%数据可视化
gscatter(data(:,1),data(:,2),label)
title("第一次迭代后的k-means聚类结果")
xlabel("x坐标")
ylabel("y坐标")

结果得到：
簇中心的坐标为：

每个簇中包含的点：

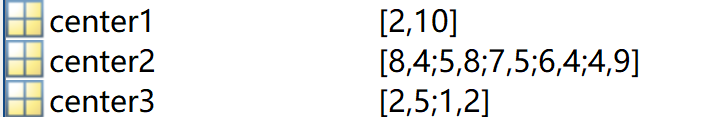
可视化结果：

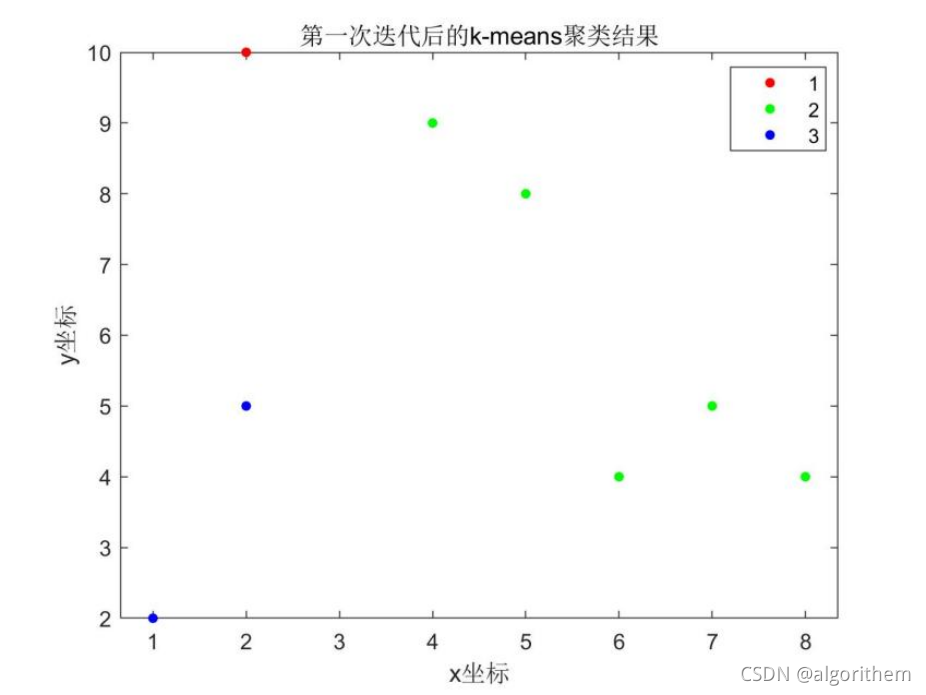
对于问题（b）

多数代码还是基于问题（a）的逻辑来做的，下面贴上代码和结果：

%%
clc; close all; clear
%%数据初始化(x1,y1)
data=xlsread("mydata.xlsx","Sheet1","B2:C9");
 
%%选取的A1，B1,C1作为簇的初始中心
A=data(1,:);
B=data(4,:);
C=data(7,:);
 
%%第一轮执行后的三个簇中心
dis=[];        %距离矩阵
D=[];
label=[];       %每个点的归属，取值1，2，3，分别表示A,B,C
[m,n]=size(data);
for i=1:m
    for j=1:m
        D(i,j)=sqrt((data(i,1)-data(j,1))^2+(data(i,2)-data(j,2))^2);
    end
end
dis=[D(1,:);D(4,:);D(7,:)];
[~,order]=sort(dis);
label=order(1,:);
 
%%开始迭代
count=0;
while(true)
    count=count+1;
    %%新的簇中心
    center1=[];
    center2=[];
    center3=[];
    for i=1:m
        if label(i)==1
            center1=[center1;data(i,:)];
        end
        if label(i)==2
            center2=[center2;data(i,:)];
        end
        if label(i)==3
            center3=[center3;data(i,:)];
        end
    end
    %%如果结果保持稳定，则退出循环
    if (isequal(A,mean(center1,1))&&isequal(B,mean(center2,1))&&isequal(C,mean(center3,1)))
        break
    end
    
    A=mean(center1,1);
    B=mean(center2,1);
    C=mean(center3,1);
    D=[];
    dis=[];
    [m,n]=size(data);
    for i=1:m
            D(1,i)=sqrt((data(i,1)-A(1,1))^2+(data(i,2)-A(1,2))^2);
            D(2,i)=sqrt((data(i,1)-B(1,1))^2+(data(i,2)-B(1,2))^2);
            D(3,i)=sqrt((data(i,1)-C(1,1))^2+(data(i,2)-C(1,2))^2);
    end
    dis=D;
    [~,order]=sort(dis);
    label=order(1,:);
end
 
%%数据可视化
% plot(center1(:,1),center1(:,2),'r0',center2(:,1),center2(:,2),'k*',center3(:,1),center3(:,2),'b-')
gscatter(data(:,1),data(:,2),label)
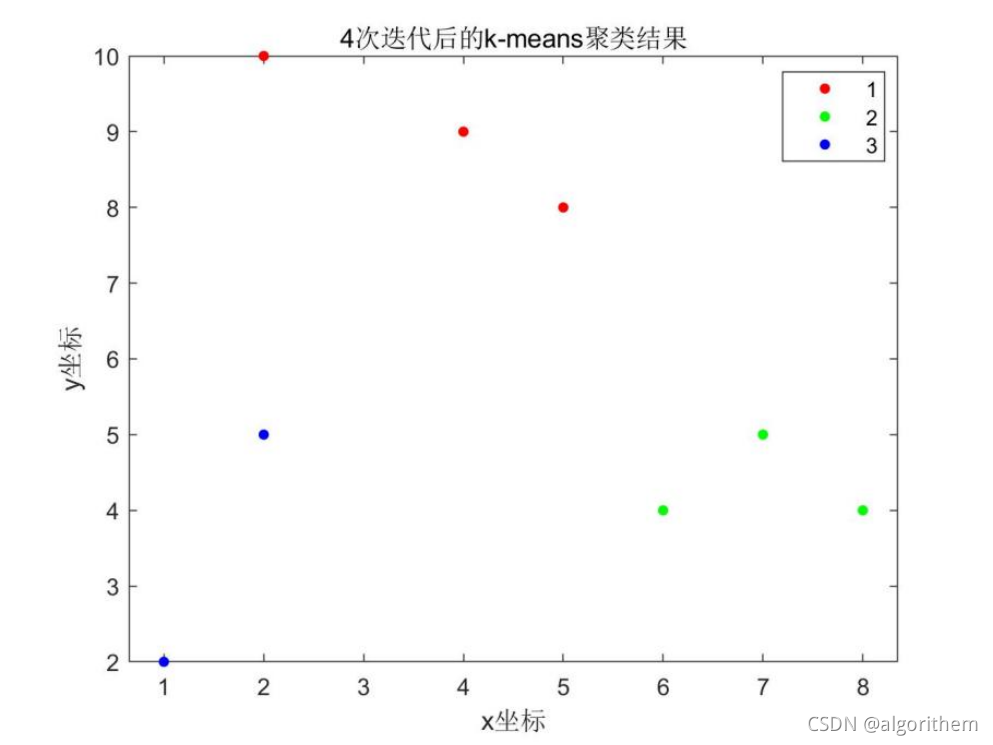
title(count+"次迭代后的k-means聚类结果")
xlabel("x坐标")
ylabel("y坐标")

一共迭代了4次
簇中心的坐标：

每个簇中包含的点：

可视化结果：

小结

祝愿大家学习相关算法上如鱼得水，上述哪里如果有问题的话，还请指教。
希望大家共创知无不言言无不尽的氛围。
以上